https://www.acmicpc.net/problem/1648
1648번: 격자판 채우기
준규는 침대에 누워서 천장을 바라보고 있었다. 천장은 격자판 모양이었고, 계속해서 천장을 바라보다 보니 이런 생각이 들었다. 세로 크기가 N이고, 가로 크기가 M인 격자판을 2x1 크기의 도미노
www.acmicpc.net
dp + 비트마스킹 문제로 넴모넴모(문제 링크) 문제와 비슷한 방식으로 해결하였습니다.
(안 푸셨으면 풀어 보시는거 추천드립니다 ㅎㅎ)
dp[x][bit] : x번 칸부터 M개의 칸의 상태가 bit일 때 x번 칸에 도미노를 놓는 경우의 수
이렇게 두고 해결하였습니다.
넴모넴모 문제는 x번 칸 이전의 M + 1개의 칸을 비트로, 이 문제는 x번 칸부터 M개의 칸을 비트로 두었습니다.
그리고 넴모넴모 문제는 x번 칸 뒤에는 채워져있지 않지만 이 문제는 채워져있을 가능성이 있어 확인을 해야하고,
0번 ~ x - 1번 칸은 모두 채워져있도록 로직을 구성하였습니다.

만약 2 * 3 격자판에 칸이 이렇게 채워져있고, x번 칸 차례라고 한다면,
x번 부터 x + (M - 1)번까지 M개의 비트는 역순으로 011로 구성됩니다.
우선 위 그림처럼 x번 칸이 이미 채워져있으면 다음 칸(x + 1)으로 넘어갑니다.
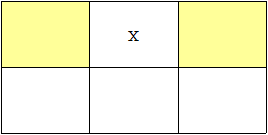
이렇게 x번 칸이 비워져있을 경우에만 1 * 2 크기나, 2 * 1 크기로 채울 수 있습니다.
위 그럼은 x + 1번 칸이 이미 채워져있으므로 1 * 2 크기는 채울 수 없습니다.
x + M번은 무조건 비어있으므로 2 * 1 크기로 채운 후 다음(x + 1)으로 넘어갈 수 있습니다.

이 그림은 x + 1번 칸이 비어있으므로 1 * 2크기를 채운 후 다음(x + 2)으로 넘어갈 수 있습니다.
x + M번은 무조건 비어있으므로 2 * 1 크기로 채운 후 다음(x + 1)으로 넘어갈 수 있습니다.
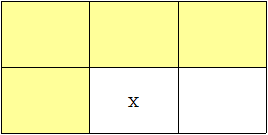
다만 이 그림처럼 맨 밑 칸은 2 * 1을 놓을 수 없으므로 맨 밑 칸이 아닐 경우에만 채워줍니다.

마지막으로 x번이 맨 오른쪽 칸일 경우에는 1 * 2크기로 채울 수 없으므로 맨 오른쪽 칸이 아닐 경우에만 채워줍니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#include <iostream>
#include <cstring>
#define MAX 14
#define MOD 9901
using namespace std;
int dp[MAX * MAX][1 << MAX];
int N, M;
int func(int x, int bit) {
if (x == N * M) return 1;
int &ret = dp[x][bit];
if (ret != -1) return ret;
ret = 0;
if (bit & 1) ret = func(x + 1, (bit >> 1));
else {
if (x / M != N - 1) ret = func(x + 1, (bit >> 1) | (1 << (M - 1)));
if (x%M != M - 1 && !(bit & 2)) ret = (ret + func(x + 2, bit >> 2)) % MOD;
}
return ret;
}
void input() {
cin >> N >> M;
memset(dp, -1, sizeof(dp));
}
int main() {
cin.tie(NULL); cout.tie(NULL);
ios::sync_with_stdio(false);
input();
cout << func(0, 0) << '\n';
return 0;
}
|
cs |
'algorithm > dp' 카테고리의 다른 글
| boj 1135 뉴스 전하기 (0) | 2021.11.15 |
|---|---|
| boj 17090 미로 탈출하기 (0) | 2021.06.27 |
| boj 14700 넴모넴모 (Hard) (0) | 2021.06.22 |
| boj 1311 할 일 정하기 1 (0) | 2021.06.21 |
| boj 1577 도로의 개수 (0) | 2021.06.20 |