10942번: 팰린드롬?
총 M개의 줄에 걸쳐 홍준이의 질문에 대한 명우의 답을 입력으로 주어진 순서에 따라서 출력한다. 팰린드롬인 경우에는 1, 아닌 경우에는 0을 출력한다.
www.acmicpc.net
팰린드롬이란 앞에서 읽을 때와 뒤에서 읽을 때와 같은 것을 의미합니다.

먼저 양쪽 끝을 기준으로 하나씩 확인하는 방법입니다.

양쪽 끝을 기준으로 한 칸씩 중간으로 이동하면서 확인하는 방법입니다. 이를 이용하면 쉽게 팰린드롬인지 파악할 수 있습니다.
하지만 문제에서 입력으로 x, y가 주어지며 이는 x번째 수 ~ y번째 수로 구성된 수열이 팰린드롬인지 묻는 쿼리가 M개 주어지며 1<= M <= 1000000입니다.
수열의 크기가 N(1 <= N <= 2000)이므로 O(NM)의 시간이 소요되며 위의 방법으로는 당연히 시간초과가 발생합니다.
다른 방법으로는 dp를 이용하는 방법입니다.
주어진 수열의 각 구간의 팰린드롬 여부를 미리 구해놓고, 쿼리가 주어지면 저장된 값을 출력만 하면되는 방법입니다.
각 구간의 팰린드롬 여부는 O(N^2)시간에 해결할 수 있고, 쿼리가 주어지면 O(1)시간에 해결할 수 있습니다.
그러면 총 시간복잡도는 O(N^2)가 되므로 문제해결이 가능합니다.
dp[x][y]: x번째 수 ~ y번째 수로 구성된 수열이 팰린드롬인지 여부
[dp[x][y]이 팰린드롬인지 확인하는 방법]
수열의 크기가 작은 부분에서 큰 부분으로 확대시키면서 팰린드롬 여부를 구해줍니다.
1. 길이가 1인 수열 ex) 1
2. 길이가 2인 수열 ex) 11
3. 길이가 3 이상의 수열 ex) 121, 1221, 12321
============================================================
1, 2번은 직접 비교하여 구할 수 있습니다.
3번은 아래의 방법을 사용합니다.
1. 팰린드롬인 경우

1. 2332의 왼쪽 끝의 숫자(2)와 오른쪽 끝의 숫자(2)가 2로 같습니다.
2. 양 끝 숫자들로 둘러쌓인 또다른 부분수열인 33역시 팰린드롬입니다.
이 두가지가 모두 만족하여 2332는 팰린드롬입니다.
2 - 1. 팰린드롬이 아닌 경우

1. 2232의 왼쪽 끝의 숫자(2)와 오른쪽 끝의 숫자(2)가 2로 같습니다.
2. 양 끝 숫자들로 둘러쌓인 또다른 부분수열인 23은 팰린드롬이 아닙니다.
이 두가지 중 2번이 만족하지 않아 2232는 팰린드롬이 아닙니다.
2 - 2. 팰린드롬이 아닌 경우
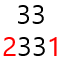
1. 2331의 왼쪽 끝의 숫자(2)와 오른쪽 끝의 숫자(1)이 다릅니다.
2. 양 끝 숫자들로 둘러쌓인 또다른 부분수열인 33은 팰린드롬입니다.
이 두가지 중 1번이 만족하지 않아 2331은 팰린드롬이 아닙니다.
위의 경우를 고려하여 구현하면 되겠습니다!
[C++]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
#include <iostream>
using namespace std;
int list[2001], dp[2001][2001];
int N, M;
void solve() {
int x, y;
while (M--) {
cin >> x >> y;
cout << dp[x][y] << '\n';
}
}
void func() {
for (int i = 2; i < N; i++) {
for (int j = 1; j <= N - i; j++) {
if (dp[j + 1][j + i - 1] && (list[j] == list[j + i])) {
dp[j][j + i] = 1;
}
}
}
}
void input() {
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> list[i];
dp[i][i] = 1;
if (list[i - 1] == list[i]) dp[i - 1][i] = 1;
}
cin >> M;
}
int main() {
cin.tie(NULL); cout.tie(NULL);
ios::sync_with_stdio(false);
input();
func();
solve();
return 0;
}
|
cs |
[Java]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer st;
static int dp[][] = new int[2001][2001];
static int list[] = new int[2001];
static int N, M;
static void solve() throws Exception {
StringBuffer sb = new StringBuffer();
int l, r;
st = new StringTokenizer(br.readLine());
M = Integer.parseInt(st.nextToken());
while (M-- > 0) {
st = new StringTokenizer(br.readLine());
l = Integer.parseInt(st.nextToken());
r = Integer.parseInt(st.nextToken());
sb.append(dp[l][r]).append("\n");
}
System.out.println(sb.toString());
}
static void func() {
for (int i = 2; i < N; i++) {
for (int j = 1; j + i <= N; j++) {
if (list[j] == list[j + i] && dp[j + 1][j + i - 1] == 1) {
dp[j][j + i] = 1;
}
}
}
}
static void input() throws Exception {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
list[i] = Integer.parseInt(st.nextToken());
dp[i][i] = 1;
if (list[i - 1] == list[i])
dp[i - 1][i] = 1;
}
}
public static void main(String[] args) throws Exception {
input();
func();
solve();
}
}
|
cs |
'algorithm > dp' 카테고리의 다른 글
| boj 1695 팰린드롬 만들기 (0) | 2021.03.20 |
|---|---|
| boj 9177 단어 섞기 (0) | 2021.03.19 |
| boj 17404 RGB거리 2 (0) | 2021.02.28 |
| boj 2616 소형기관차 (0) | 2021.02.27 |
| boj 11049 행렬 곱셈 순서 (0) | 2021.02.20 |